Part of the reason a constant ambient value has been accepted for so long (other than the cost of replacing it) is that diffuse interreflection changes only gradually over surfaces. Thus, the contrast-sensitive eye usually does not object to the loss of subtle shading that accompanies an ambient approximation. However, the inaccuracies that result are a problem if one wants to know light levels or see the effects of daylight or indirect lighting systems.
Since indirect lighting changes gradually over surfaces, it should be possible to spread out this influence over many pixels to obtain a result that is smooth and accurate at a modest sampling cost. This is exactly what we have done in Radiance. The original method for computing and using cached irradiance values [25] has been enhanced using gradient information [28].
The basic idea is to perform a full evaluation of Equation (1) for indirect diffuse contributions only as needed, caching and interpolating these values over each surface. Direct and specular components are still computed on a per-pixel basis, but hemispherical sampling occurs less frequently. This gives us a good estimate of the indirect diffuse contribution when we need it by sending more samples than we would be able to afford for a pixel-independent calculation. The approach is effectively similar to finite element methods that subdivide surfaces into patches, calculate accurate illumination at one point on each patch and interpolate the results. However, an explicit mesh is not used in our method, and we are free to adjust the density of our calculation points in response to the illumination environment. Furthermore, since we compute these view-independent values only as needed, separate form factor and solution stages do not have to complete over the entire scene prior to rendering. This can amount to tremendous savings in large architectural models where only a portion is viewed at any one time.
Figure 1 looks down on a diffuse sphere in a room with indirect lighting only. A blue dot has been placed at the position of each indirect irradiance calculation. Notice that the values are irregularly spaced and denser underneath the sphere, on the sphere and near the walls at the edges of the image. Thus, the spacing of points adapts to changing illumination to maintain constant accuracy with the fewest samples.
To compute the indirect irradiance at a point in our scene, we send a few hundred rays that are uniformly distributed over the projected hemisphere. If any of our rays hits a light source, we disregard it since the direct contribution is computed separately. This sampling process is applied recursively for multiple reflections, and it does not grow exponentially because each level has its own cache of indirect values.
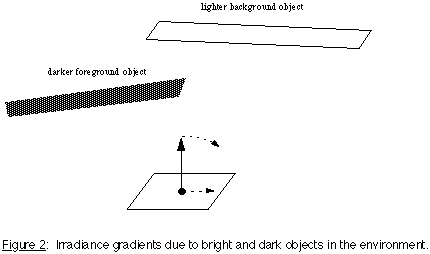
Our hemisphere samples not only tell us the total indirect illumination, they also give us more detailed information about the locations and brightnesses of surfaces visible from the evaluation point. This information may be used to predict how irradiance will change as a function of point location and surface orientation, effectively telling us the first derivative (gradient) of the irradiance function. For example, we may have a bright reflecting surface behind and to the right of a darker surface as shown in Figure 2. Moving our evaluation point to the right would yield an increase in the computed irradiance (i.e. the translational gradient is positive in this direction), and our samples can tell us this. A clockwise rotation of the surface element would also cause an increase in the irradiance value (i.e. the rotational gradient is positive in this direction), and our hemisphere samples contain this information as well. Formalizing these observations, we have developed a numerical approximation to the irradiance gradient based on hemisphere samples. Unfortunately, its derivation does not fit easily into a general paper, so we refer the reader to the original research [28].
Figure 3a,b. Plots showing the superiority of gradient interpolation for indirect irradiance values. The reference curve is an exact calculation of the irradiance along the red line in Figure 1. The linear interpolation is equivalent to Gouraud shading between evenly spaced points, as in radiosity rendering. The Hermite cubic interpolation uses the gradient values computed by Radiance, and is not only smoother but demonstrably more accurate than a linear interpolation.Knowing the gradient in addition to the value of a function, we can use a higher order interpolation method to get a better irradiance estimate between the calculated points. In effect, we will obtain a smoother and more accurate result without having to do any additional sampling, and with very little overhead. (Evaluating the gradient formulas costs almost nothing compared to computing the hemisphere samples.)
Figure 3a shows the irradiance function across the floor of Figure 1, along the red line. The exact curve is shown overlaid with a linearly interpolated value between regularly spaced calculation points, and a Hermite cubic interpolation using computed gradients. The cubic interpolation is difficult to separate from the exact curve. Figure 3b shows the relative error for these two interpolation methods, clearly demonstrating the advantage of using gradient information.
Caching indirect irradiances has four important advantages over radiosity methods. First, no meshing is required, since a separate octree data structure is used to hold the calculated values. This lifts restrictions on geometric shapes and complexity, and greatly simplifies user input and scene analysis. Second, we only have to compute those irradiances affecting the portion of the scene being viewed. This speeds rendering time under any circumstance, since our view-independent values may be reused in subsequent images (unlike values computed with importance-driven radiosity [20]). Third, the density of irradiance calculations is reduced at each level of interreflection, maintaining constant accuracy while reducing the time required to compute additional bounces. Fourth, the technique adapts to illumination by spacing values more closely in regions where there may be large gradients, without actually using the gradient as a criterion. This eliminates errors that result from using initial samples to decide sampling density [12], and improves accuracy overall. The gradient is used to improve value interpolation, yielding a smoother and more accurate result without the Mach-bands that can degrade conventional radiosity images.