Gregory J. Ward
ABSTRACT
We present a simple technique for improving the efficiency of ray tracing in scenes with many light sources. The sources are sorted according to their potential contribution, and only those sources whose shadows are above a specified threshold are tested. The remainder are added into the result in proportion to a statistical estimate of their visibility. The algorithm requires very little storage, and produces no visible artifacts.
1. Introduction
Since ray tracing was introduced to the computer graphics community by Whitted [Whitted80] it has proven to be a powerful approach to difficult problems in global illumination [Wallace89] [Shirley90]. In particular, the view-dependent nature of ray tracing offers important advantages over view-independent radiosity solutions for non-diffuse (ie. interesting) environments [Immel86] [Kajiya86]. However, there are illumination problems where the approach of a pixel-independent calculation is a liability rather than an asset. Rendering scenes with significant diffuse interreflection is one such problem [Ward88] [Heckbert90], and scenes with many light sources represent another. Unfortunately, these are both common occurrences in the real world, and as such cannot be ignored if rendering realism is the goal.
Visibility testing is the most time-consuming part of a global illumination calculation, and the visibility of light sources is particularly important since they determine the initial lighting distribution. If we could assume that all of the light sources were visible at every point, the calculation would reduce to a few simple operations. Unfortunately, it is almost always necessary to check for occlusions from light sources (ie. perform shadow testing). Spatial subdivision techniques for accelerating ray tracing are essential for general efficiency [Glassner84], but shadow testing still remains the single most time-consuming portion of most ray traced renderings.
Haines introduced a spatial sorting technique to minimize the amount of time required for shadow testing in a polygonal environment with point light sources [Haines86]. The scene is sorted according to the polygons visible from each source, and shadow testing takes advantage of the fact that it does not matter where obstruction occurs between the source and test point in question. (Normally, ray tracing algorithms are optimized to find the first intersection -- here we just want to find some intersection.) Although this approach offers significant reductions in calculation time, it requires O(N*M) storage, where N is the number of light sources and M is the number of polygons in the scene. These storage costs can get out of hand for scenes with tens of thousands of surfaces and more than a hundred light sources. (It should be noted that curved surfaces can be included using convex polyhedral bounding volumes, though implementation of the algorithm becomes more difficult.)
In this paper we present a very simple approach to light source testing that trades accuracy, rather than storage, for increased speed. The algorithm has been tested on many different models and has been found to be robust and reliable, offering speed increases between 20% and 80% in most environments. Furthermore, the user can control the accuracy and reliability of the technique, adapting it to suit his or her requirements. If the user specifies an error bound of zero, the algorithm degenerates to the base case with very little overhead, providing straightforward validation and comparison of results.
2. Concept
In scenes with many light sources, only a few will create strong shadows in any one part of the scene. These will generally be the sources with the highest concentration of light in that section due to source brightness, direction and proximity. The remainder of the light sources will contribute, but without causing any significant contrast gradients. Since it is contrast that stimulates the human visual system, lack of contrast translates to low importance for visual studies.
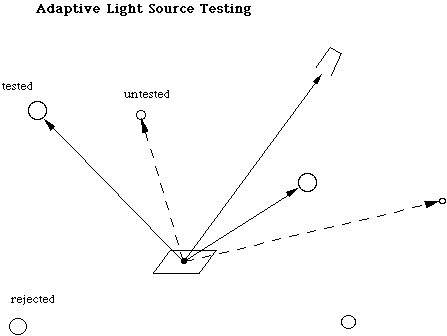
This observation leads to a simple optimization: we can perform shadow testing on the sources with the highest potential contributions first, and quit testing when the remainder of the contributions is below some threshold (see Figure 1). By itself, this approach can guarantee an absolute error below a given threshold. However, it is still not optimal since we do not know what to do with the remainder of untested sources. Do we add them all in, leave them all out, or add in some and leave out others? How we answer this question in effect determines the efficiency of our algorithm. If we do a good job guessing at the visibility of light sources we do not test, our results will be very close to those of the full calculation without the associated cost.

Figure 1. The brightest sources are tested first, and a fraction of the potential contributions from untested sources are added in as an approximation.
We turn to statistics to provide us with a reasonable estimate of visibility for our untested light sources. If a light source is untested, we use the fraction of hits to that source as a multiplier for its contribution. (We maintain these statistics as light sources are tested. Thus, our estimate will be crude at the beginning and improve during the course of the calculation.) We use the fraction of sources hit for the tested sources at this point as a second multiplier. In terms of random variables:
The probability of seeing source i at p is:
P(Xi,Yp) = P(Xi) P(Yp)
where: Xi is a random variable for hits on source i
Yp is a random
variable for hits at point p
This assumes that source visibility at our test point is independent of visibility at each source. This is of course an approximation, but it holds well for interior spaces, where obstructions are many near the floor and the ceiling, and few in between.
Note that we do not test sources based on the probability that they are visible. Rather, we use the probabilities for untested sources as a multiplier to approximate their contribution. A weak source deemed unworthy of shadow testing at a particular point is not used or thrown out based on a random variable -- such a procedure would result in visible noise that is completely unnecessary. Using probabilities as coefficients in the way given here yields smooth shading and visually pleasing results without compromising accuracy.
3. Algorithm
We can refine our algorithm by adding a parameter to control the reliability of our source calculation. If we are not terribly concerned about accuracy but want a nice picture, we can stop source testing as soon as the next contribution is below some threshold. This will not guarantee numerical accuracy, but it will at least guarantee that all visually significant shadows will be tested. We introduce a variable called certainty, c, that can be set continuously between 0 and 1 to control reliability. A value of 0 for c means that the potential contribution of any untested source is below the tolerance, t, thus guaranteeing only contrast, and a value of 1 for c means that the sum total of all untested sources is below t, thus guaranteeing absolute accuracy.
The algorithm can be written as the following steps (see below for comments):
1) Compute potential contributions from all light sources in front of this point.
A
2) Sort the contributions in descending order.
3) Compute r(i), the sum of the next Nc contributions smaller than i, where N is the number of light sources and c is the certainty.
4) Initialize the sum, S, hits, v, and
tests, w, to 0.
Foreach contribution in our sorted list
do
B
if S t > r(i) then
go to step 5
increment
our test counter, w
increment the test counter for source i,
w(i)
C
if source i is visible from this point then
increment our hit counter, v
increment the hit counter for source
i, v(i)
add contribution for source i to
S
5) Foreach untested contribution do
D
multiply contribution by v/w and v(i)/w(i)
add
weighted contribution to S
6) Return S
Comments:
A This is the only part of the calculation that is extra beyond standard light source testing. The quicker sort algorithm (qsort C library routine) is fast enough in comparison with the rest of the calculation that the extra time is insignificant.
B S is the sum of visible contributions tested so far, thus the test S t > r(i) checks to see if the remaining Nc contributions are below the threshold. If true, then we have satisfied our visibility testing requirements and can go on to approximate the remaining contributions to S.
C This is the actual source visibility test, and this is where the real cost of the direct calculation is incurred. The whole point is to minimize the number of light sources that must be tested here for visibility (see B above).
D The ratios, v/w and v(i)/w(i), are the estimated probabilities of seeing any source from our test point and seeing source i from any point, respectively.
4. Results
The graphs in Figure 3 show the adaptive shadow testing algorithm's performance for the model shown in Figure 2, a conference room with 24 ceiling-mounted fluorescent fixtures with high angle cutoff (resulting from small cube parabolic louvres).

Figure 2. Conference room model used to test shadow algorithm.
Figure 3a shows the fraction of light sources tested for visibility when the algorithm is applied with different values of t and c. Note that with a target accuracy (tolerance) of 0, all of the candidate light sources are tested no matter what value is given for certainty.
The overall rendering time is roughly proportional to the fraction of light sources tested. If an average of 50% of the light sources are tested, the rendering takes a little bit more than 50% as long. The "little bit more" is the time required to follow non-shadow rays (eg. eye rays) and compute their shading plus the time required to calculate the potential contributions of untested sources.
Figures 3b and 3c show the average and maximum error corresponding to the different settings, as compared with a fully tested source calculation. In this example, the average error is always kept below the requested tolerance, and even the maximum error (most deviant pixel) is kept within limits for certainties better than 25%.
What happens to the calculation as we increase the number of light sources? For the purposes of comparison, we used the same scene and replaced each rectangular source with 8 smaller sources and repeated the tests. The resulting fraction of shadow tests for this modified scene is shown in Figure 4. The most noticeable difference is the overall drop in the fraction of sources tested, which indicates that the algorithm's performance improves as light sources are added to the scene. (It still takes longer of course.) Also, there is a larger spread between the different certainties. It should be noted that further improvement in performance would be apparent if instead of increasing the number of sources in the same locations, the overall dimension of the space were increased. A larger room with the same ceiling height would have proportionally more sources with small potential contributions that would be excluded from visibility testing by our algorithm. In fairness, though, the same cannot be said for multiple floors with all light sources turned on, since the lights in the floors above would be tested even though they cannot possibly contribute to the image. In general, it is better to exclude such non-contributing sources from the calculation.
Figure 5a shows the same conference room with floating furniture -- a more difficult case for the shadow testing algorithm. Figure 5b shows the same scene rendered with adaptive shadow testing using a tolerance of 20% and a certainty of 50%. This resulted in an 80% reduction in shadow testing with an average pixel error of less than 5%. Figure 5c shows the squared error between the two images (times 100). The errors are largest where surfaces are fully illuminated, because the algorithm uses statistics that say those areas probably do not see all of the light sources when in fact they do. However, these errors are not very visible because the eye is not good at making absolute comparisons.
Figure 6 shows the fraction of shadow tests for 192 high-cutoff sources in the scene with floating furniture. Compared to Figure 4, there is a greater cost associated with the certainty parameter. Figure 7a shows the same test with diffuse (cosine emitting) sources. Here we see the "pretty bad case" performance of our algorithm (as opposed to "worst case"). The certainty plays an even greater role here since diffuse light sources can contribute significant amounts in shadowed areas even when they are on the opposite side of the room.
Figure 7b and 7c show the average and maximum error for diffuse sources and floating furniture, and this is where we see the true performance of our statistical visibility approximation. For certainties above 25%, the average error is maintained within the specified tolerance. This means that even though visibility is not being tested sufficiently, the approximation is coming up with reasonable guesses for the untested sources most of the time. The maximum error, however, falls out of range for 50% certainty, and becomes quite large for 1% certainty. This points out the importance of setting the certainty value with care. If the specified tolerance is truly required, a high certainty should be given. If nice-looking shadows are all that matter, a low certainty will maintain proper contrast boundaries while minimizing tests for shadows that would be invisible to the eye.
5. Conclusion
We have presented a simple optimization for the calculation of the direct light component in global illumination computations using ray tracing. The most important sources for a point are tested first, and less important sources are only tested if their visibility is deemed important to the calculation. If none of the sources is visible, all of the sources that could contribute are tested for visibility. Thus it is fruitless to apply this technique inside of walls and under carpeting.
An important feature of this algorithm is that it avoids stochastic sampling. In computer graphics, smooth shading is valued as highly as correct results, and it is best to avoid random noise if the raw artifacts are not visible. By choosing contrast as the primary criteria, our calculation manages to avoid offending the eye in its speed-for-accuracy tradeoff.
Although contrast is a good visual criterion, it does not determine absolute accuracy in a lighting simulation. Thus, a certainty parameter is provided to indicate the relative importance of accuracy. Absolute accuracy can be guaranteed by the algorithm at a slightly higher cost. However, the statistical estimate of source visibility works well enough that such a guarantee is not really necessary.
Another advantage of the source visibility approximation is that it does not rely on point sampling coherence. The calculations can take place at random locations throughout the scene with no loss in speed. Many light source optimizations rely on the next point being close to the last one, as might hold in a simple scanline traversal of an image. Unfortunately, this is not usually the case in a global illumination calculation, where rays are followed all over the scene in no particular order. By maintaining global statistics on source visibility, our algorithm makes use of information that is available and applicable at any point in the scene. Initial tests will have less information to go on, but the statistics build quickly and coherently in the places where they are needed so that artifacts are not visible.
The overhead costs of the algorithm are minimal. The storage overhead is a few additional words per light source for keeping track of test and hit counts. The only additional computation required is the sorting of the potential light source contributions before each test sequence, and we have found this step to be inconsequential in all of the test cases we have studied.
A chief feature of this adaptive light source testing algorithm is its simplicity. In less than a page of C code, a procedure that provides up to a 70% reduction in calculation time can be written. Furthermore, the approach is orthogonal to most other global illumination techniques, and can be added to existing direct light calculations and optimizations.
One optimization that works very well with this algorithm is to relax the tolerance for spawned rays that contribute less to the final pixel value. Other variations such as stochastic sampling of area sources for accurate penumbras work very well also.
Acknowledgements
Thanks goes to Anat Grynberg, who created the conference room model, and to Charles Erhlich, whose abuse of my rendering software compelled me to develop a better direct calculation in the first place. Thanks also to Peter Shirley and Erik Jansen for their helpful feedback. This work was supported by the Assistant Secretary for Conservation and Renewable Energy, Office of Building Energy Research and Development, Buildings Equipment Division of the U.S. Department of Energy under Contract No. DE-AC03-76SF00098. Current research in this area is being sponsored by the LESO Solar Energy Group at the Ecole Polytechnique Federale de Lausanne in Switzerland.
Bibliography
[Glassner84] A. Glassner, "Space Subdivision for Fast Ray Tracing," IEEE Computer Graphics and Applications, vol. 4, no. 10, October 1984, pp. 15-22.
[Haines86] E. Haines, D. Greenberg, "The Light Buffer: A Shadow-Testing Accelerator," IEEE Computer Graphics and Applications, September 1986, pp. 6-16.
[Heckbert90] P. Heckbert, "Adaptive Radiosity Textures for Bidirectional Ray Tracing," Computer Graphics, vol. 24, no. 4, August 1990, pp. 145-154.
[Immel86] D. Immel, D. Greenburg, M. Cohen, "A Radiosity Method for Non-Diffuse Environments,'' Computer Graphics, vol. 20, no. 4, August 1986, pp. 133-142.
[Kajiya86] J. Kajiya, J., "The Rendering Equation,'' Computer Graphics, vol. 20, no. 4, August 1986, pp. 143-150.
[Shirley90] P. Shirley, "A Ray Tracing Method for Illumination Calculation in Diffuse-Specular Scenes," Proceedings of Graphics Interface '90, May 1990, pp. 205-212.
[Wallace89] J. Wallace, K. Elmquist, E. Haines, "A Ray Tracing Algorithm for Progressive Radiosity," Computer Graphics, vol. 21, no. 4, July 1989, pp. 315-324.
[Ward88] G. Ward, F. Rubinstein, R. Clear, "A Ray Tracing Solution for Diffuse Interreflection," Computer Graphics, vol. 22, no. 4, August 1988, pp. 85-92.
[Whitted80] T. Whitted, "An Improved Illumination Model for Shaded Display,'' Communications of the ACM, vol. 23, no. 6, June 1980, pp. 343-349.